 |
 |
 |
 |
Beide Naturwissenschaften sind eng miteinander verflochten und ich möchte hier keine starren, umständlichen Definitionen geben, die im Zeitalter interdisziplinären Forschens und Arbeitens ohnehin fragwürdig erscheinen, sondern ein paar Gedanken dazu skizzieren.

Die Frage nach dem Wesen der Welt und uns selbst, ist wohl zutiefst menschlich.
Mathematik und Physik können uns helfen darauf Antworten zu finden und die Dinge, so wie sie für uns erfahrbar sind, besser zu verstehen.

Zahlensymbole und die Anfänge von Zählverfahren lassen sich ca. 50 000 Jahre zurück belegen.
Auch bei einigen Tierarten wurde eine gewisse Art Verständnis für Mengen und Zahlen nachgewiesen.
Somit könnte man die Frage stellen, ob Mathematik entdeckt oder erfunden wurde.

Systematisch wurde Mathematik wohl seit ca. 3000 vor Chr. betrieben.
Das Zählen der Gruppenmitglieder, der Tiere, später das Vermessen der Felder, die Architektur und schließlich der Umgang mit Geld erforderten die Entwicklung ständig komplexerer mathematischer Methoden.
Astronomische Beobachtungen konnten schon früh mit Hilfe der Mathematik und Physik erhellt werden.
Pythagoras (ca. 570 v.Chr.) erkannte die Zusammenhänge zwischen Mathematik und der Harmonie in der Musik und Archimedes (ca. 270 v.Chr.) ermöglichte mit ihrer Hilfe viele neue technische Anwendungen.
Mathematik scheint gewissermassen irgendwie hinter nahezu Allem zu stecken.
Sie war immer eng mit der Naturphilosophie verbunden und Kopernikus (*1473) konnte mit ihr unser modernes Weltbild begründen.

Eine schöne Beschreibung dessen was Mathematik sein könnte gab Galileo Galilei (1564-1642):

|
 |
 |
"Das Buch der Natur ist in Mathematik geschrieben"
|
 |
 |
 |
 |
 |
Und er war es dann auch der die experimmentelle Untersuchung der Natur und deren mathematische Beschreibung entscheidend vorantrieb.
Issac Newton (1643-1727) folgte als einer der bedeutensten und ersten systematisch arbeitenden Naturwissenschaftler.

Die uns wahrnehmbare Natur der Dinge lässt sich hervorragend mit Hilfe der Mathematik und Physik beschreiben und vorhersagen.
Heute gibt es nahezu kein Tätigkeitsfeld mehr, das nicht ein gewisses Mass an mathematischen und physikalischen Kentnissen erfordert.
Der sich ständig beschleunigende Wandel in unserer Arbeitswelt wird diese Tatsache sicherlich verstärken.

Die rassante Entwicklung der modernen Physik ist bekannt, aber auch die Mathematik ist eine lebendige, sich stetig weiterentwickelnde Wissenschaft.
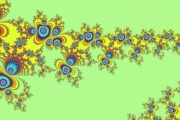
Ein Beispiel aus der Gegenwart ist die fraktale Geometrie.

Bernoit Mandelbrot (1924-2010) gab der Mathematik neue bedeutende Impulse.
Ausgehend von relativ einfachen Strukturen entstehen durch permanente Wiederholung mathematischer Operationen interessante Formen, sogenannte Fraktale.
|
 |
 |
Mandelbrotfraktale |
 |
 |







 |
 |
 |
⇒ Bilder größer zeigen
|
 |
 |
Das sind nicht nur nett anzuschauende Bilder.

Mandelbrot's Prinzip, einfache Formen immer wieder ähnlich zu reproduzieren hat noch nicht absehbare praktische Möglichkeiten.

Einige Anwendungsbeispiele:

- Antennen für Mobilfunk und schnelles mobiles Internet
- In der Grundlagenforschung der Medizin zur Beschreibung von Gefäßsystemen
für die Früherkennung
von Tumor- oder Herzerkrankungen sowie zur Untersuchung
komplexer biologischer Strukturen.
- Simulationen dreidimensionaler Landschaften und Strukturen.
- Viele Effekte in Starwars wurden z.B. damit erzeugt.

- Generell zur Beschreibung von zunächst chaotisch erscheinenden Systemen -

Dieses Prinzip ist in seiner Bedeutung für unser Weltverständnis noch nicht absehbar.
|
 |
 |
Ich hoffe, etwas Interesse geweckt und einige Vorurteile über Mathematik und Physik gemindert zu haben.
|
 |
|

